반응형
어떤 수열의 연속 부분합을 구해보자!!
어떻게 해결할 것인가?
직관적으로 떠오르는 아이디어는 단순하게 이중 for문을 돌리는 것이다. 그러나 이 방법은 O(N^2)의 시간복잡도를 가지기 때문에 효율적이지 못하다. 투 포인터를 사용하면 시간 복잡도를 O(N)까지 단축시킬 수 있다.
위 문제의 핵심은 '연속'에 있다. 연속합을 구하는 것이기 때문에 중복되는 부분이 존재한다. 말로 하면 헷갈리니깐 그림으로 보자.

위 그림에서 빨간색과 파란색의 연속된 부분합에서 형광색 부분이 중복됨을 알 수 있다. 이 사실을 잘 기억하자. 이제 투 포인터의 알고리즘을 살펴보고, 손으로 예제 한 문제를 직접 풀어보자.
[ 투 포인터 알고리즘 ]
1. 시작점(start), 끝점(end)을 -1로 초기화한다
2. 현재 부분합(sum)이 S보다 작다면 start++ 해주고 sum -= ary[start] 해준다
3. 현재 부분합(sum)이 S보다 크거나 같으면 end++ 해주고 sum += ary[end] 해준다
4. end < N 일때까지 2,3번 반복. (N은 배열의 크기)
위 알고리즘에 따라 예제 하나를 풀어보자. 연속된 수들의 부분합 중에 그 합이 S 이상이 되는 것 중, 가장 짧은 것의 길이를 구하는 예제다. 백준 1806번 예제와 동일하다.
[예제]
N = 10, S = 15
ary = [5, 1, 3, 5, 10, 7, 4, 9, 2, 8]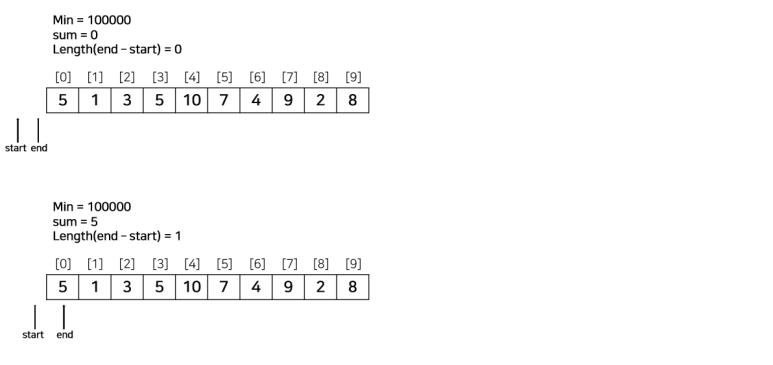
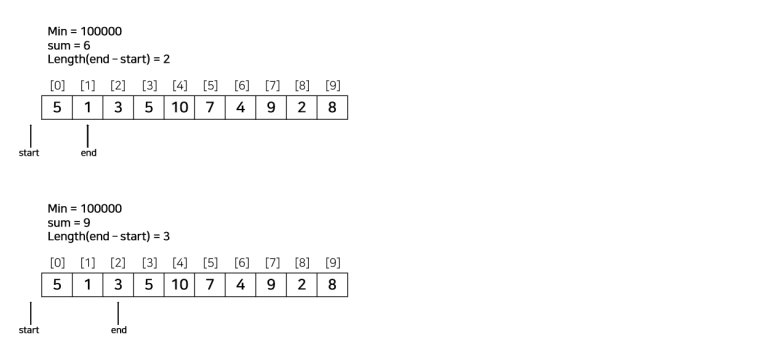
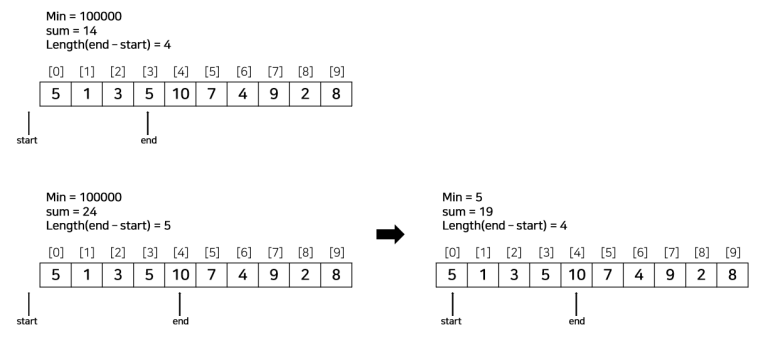
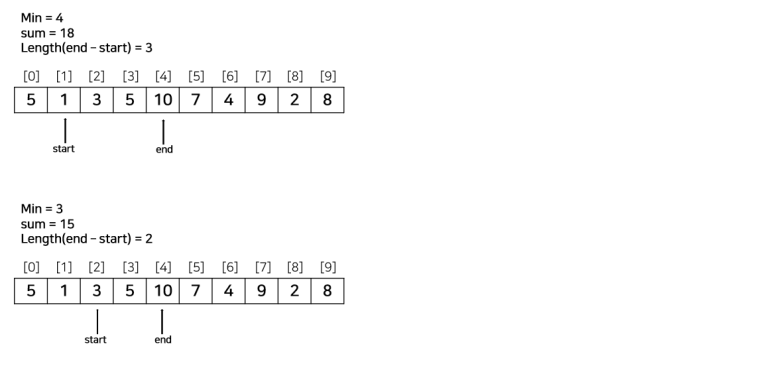
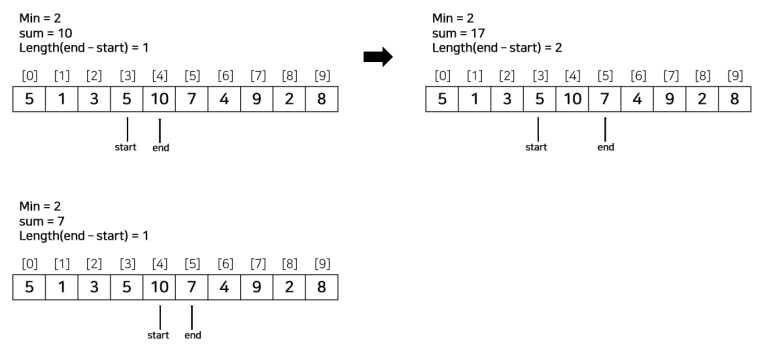
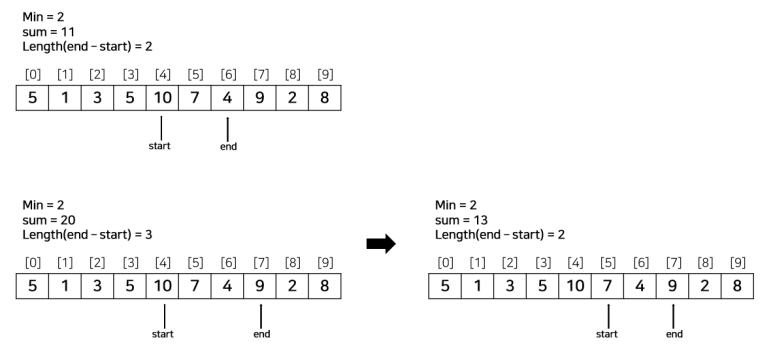
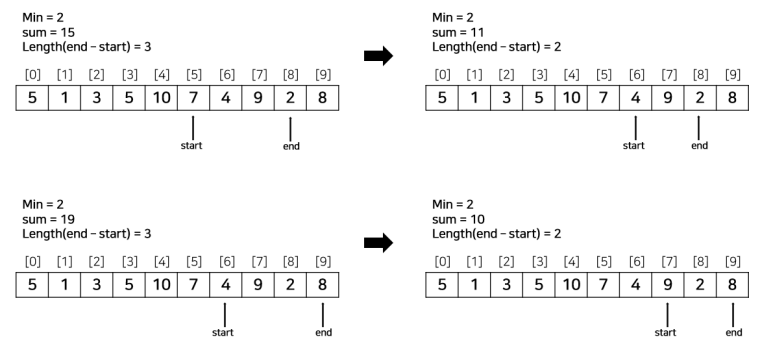
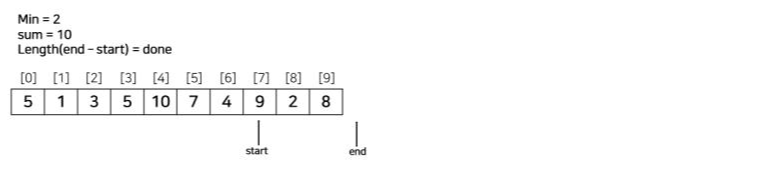
코드는 아래와 같다
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
int N, S;
cin >> N >> S;
int* ary = new int[N];
for (int i = 0; i < N; i++)
cin >> ary[i];
int start = -1, end = -1, sum = 0;
int Min = 100000;
while(end < N) {
if (sum < S) {
end++;
sum += ary[end];
continue;
}
if (sum >= S) {
Min = min(Min, end - start);
start++;
sum -= ary[start];
continue;
}
}
if (Min == 100000)
cout << 0 << endl;
else
cout << Min << endl;
delete[] ary;
return 0;
}반응형
'CS > 알고리즘' 카테고리의 다른 글
| [ 알고리즘 ] 이분탐색(Binary Search), upper_bound, lower_bound (C++) (0) | 2022.03.18 |
|---|---|
| [C++] 위상 정렬(Topology Sort) (0) | 2022.01.14 |
| [C++] 다익스트라(Dijkstra) (0) | 2022.01.14 |
| [C++] 중위 표기식을 후위 표기식으로 변환 후 계산 (0) | 2022.01.14 |
| [C++] 순열과 조합 DFS로 구현해보기 (1) | 2022.01.14 |



