1. 다익스트라의 구성
최소 거리를 구할때 사용하는 대표적인 알고리즘 '다익스트라'에 대해 알아보자. 다익스트라 알고리즘은 시작점으로부터 모든 노드까지의 최소거리를 구해준다. 다익스트라를 구현하기 위해서는 비용 배열, 방문 노드 배열, 시작점~각 노드까지의 비용 배열이 필요하다.
[ 다익스트라 구현시 필요 요소 ]
1. 비용 배열 weight(이중배열)
출발지에서 목적지로 갈 때 드는 비용을 나타내는 배열이다.
weight[3][5] = 5 // 노드3 -> 노드5 갈 때 비용이 5만큼 든다는 뜻이다.
weight[2][4] = INF // 노드2 -> 노드4 갈 때 비용이 무한만큼 든다는 뜻이다.
2. 방문 노드 배열 visit
방문한 노드를 확인하는 배열이다.
visit[3] = true // 노드3을 이미 방문했다는 뜻이다.
3. 시작점~노드 배열 dist
시작 노드로부터 각 노드까지의 비용 배열이다.
dist[1] = 3 // 시작점~노드1 까지 가는데 비용이 총 3만큼 든다.
dist[2] = 5 // 시작점~노드2 까지 가는데 비용이 총 5만큼 든다.
dist[5] = INF // 시작점~노드5 까지 가는데 비용이 무한이다.
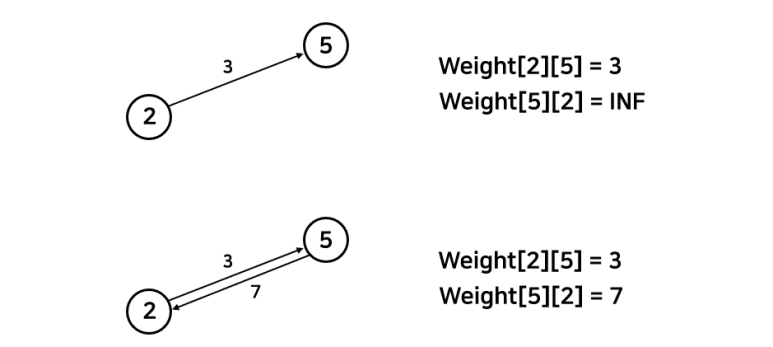
다익스트라에서 노드간의 연결은 wiehgt의 값으로 판단한다. 특정 값이 있으면 연결되어 있다는 뜻이고, 무한값(INF)이면 연결되지 않았다는 뜻이다. 실제로 무한 값은 아니고 자료형의 최대값으로 보는 게 적절하다. 노드 간의 방향성도 표현할 수 있다. 단방향, 양방향을 아래와 같이 표현할 수 있다.
2. 다익스트라 알고리즘 직접 해보기
이제 바로 다익스트라 알고리즘을 살펴보자.
[ 다익스트라 알고리즘 ]
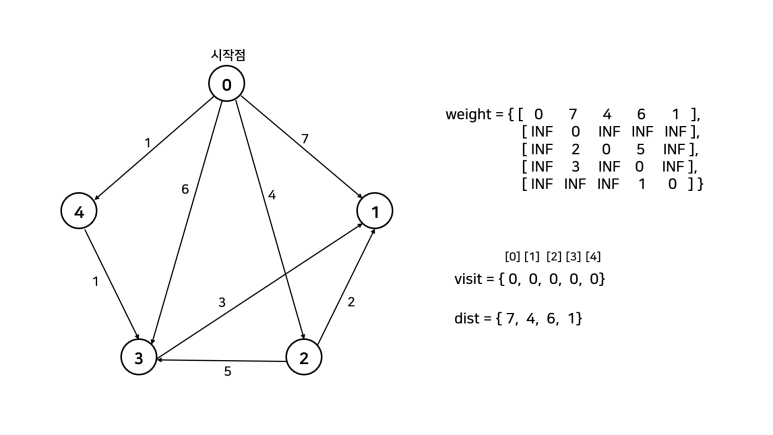
1. dist 배열을 weight[시작점 노드]의 값들로 초기화시켜준다
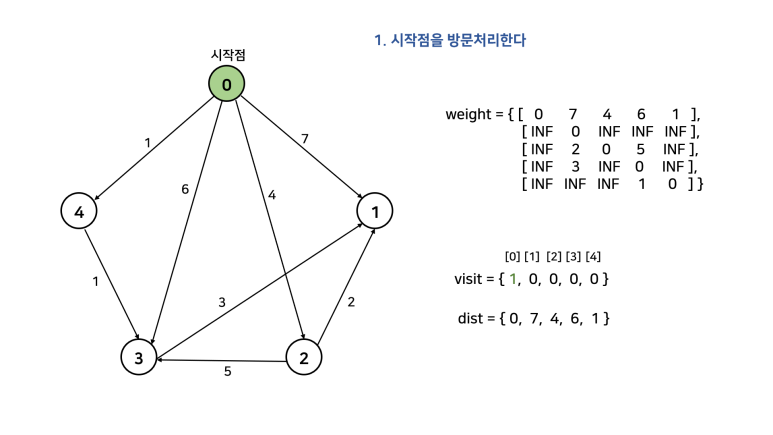
2. 시작점을 방문처리 한다
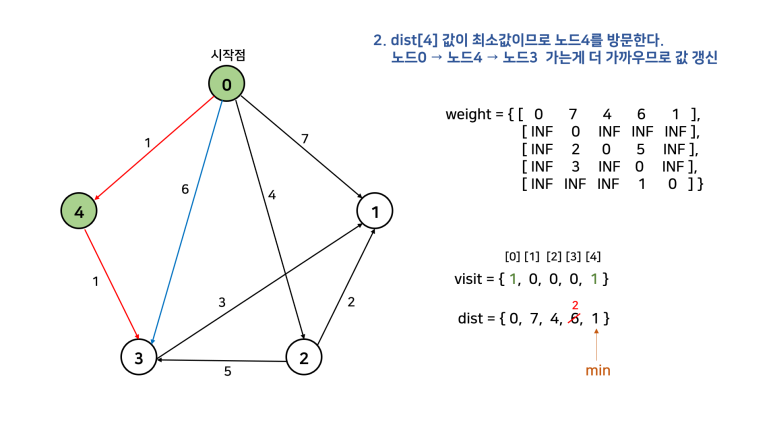
3. dist 배열에서 최소비용노드를 찾고 방문처리한다. 단, 이미 방문한 노드는 제외.
4. 최소비용노드를 거쳐갈지 말지 고려해서 dist 배열을 갱신한다. 단, 이미 방문한 노드는 제외.
5. 모든 노드를 방문할때까지 3-4 반복
이를 한 문장으로 정리하면, "방문하지 않은 노드 중 가장 작은 dist를 가진 노드를 방문하고, 그 노드와 연결된 다른 노드까지의 거리를 계산한다"이다. 먼저 손으로 직접 풀어보고 코드를 살펴보자. 아래 그림에서 시작점을 0으로 두고 진행한다. 참고로, 자기 자신으로 가는 경우 비용을 0으로 해도 되고, INF로 해도 된다. 그 이유는 방문을 먼저 하고 dist를 탐색하기 때문이다. dist를 탐색할 때는 방문한 노드는 고려대상에서 제외된다.
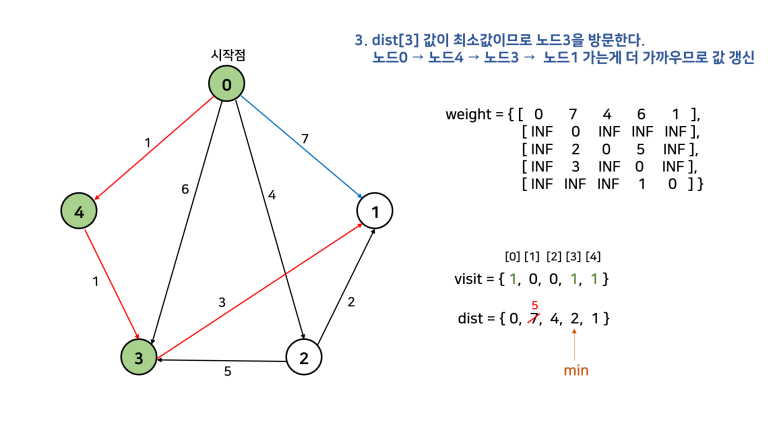
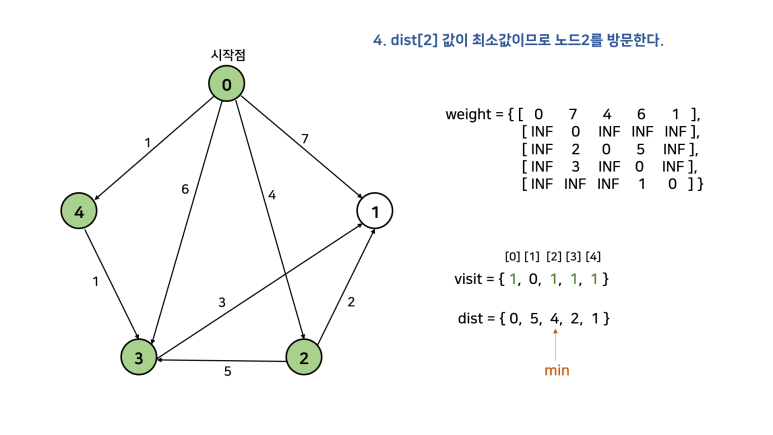
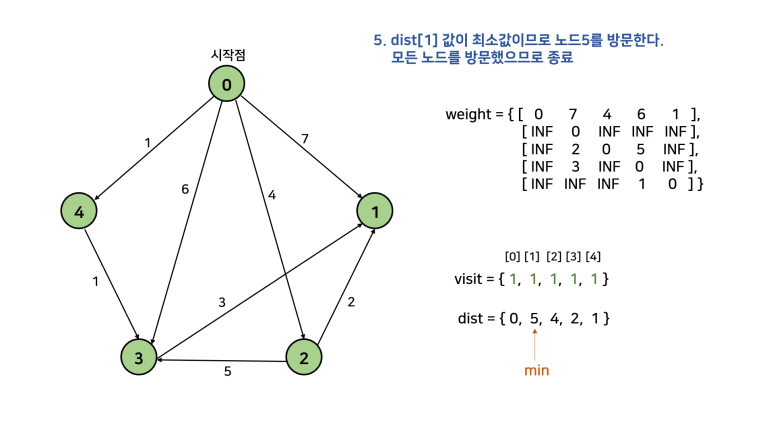
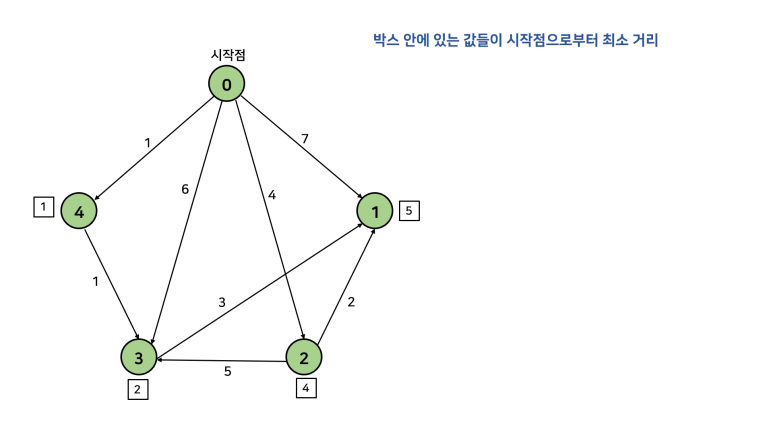
이를 그대로 코드로 구현하면 아래와 같다.
#include <iostream>
#define INF 1000000000
#define N 5
using namespace std;
int weight[N][N] = { { 0,7,4,6,1},
{ INF,0,INF,INF,INF},
{ INF,2,0,5,INF},
{ INF,3,INF,0,INF},
{ INF,INF,INF,1,0} };
bool visit[N];
int dist[N];
int min_node;
int get_small_node() {
// 최소비용노드 탐색 함수
int min = INF;
int minpos = 0;
for (int i = 0; i < N; i++) {
if (dist[i] < min && !visit[i]) {
min = dist[i];
minpos = i;
}
}
return minpos;
}
void dijkstra(int start) {
for (int i = 0; i < N; i++) {
dist[i] = weight[start][i];
}
visit[start] = true;
for (int repeat = 0; repeat < N - 1; repeat++) {
min_node = get_small_node(); // 최소비용노드 탐색
visit[min_node] = true; // 최소비용노드 방문처리
for (int i = 0; i < N; i++) {
// 방문하지 않은 노드 중에, 시작점이 최소비용노드를 경유하는게
// 더 가까우면 값 갱신
if (!visit[i])
if (dist[min_node] + weight[min_node][i] < dist[i])
dist[i] = dist[min_node] + weight[min_node][i];
}
}
}
int main() {
dijkstra(0);
for (int i = 0; i < N; i++)
cout << dist[i] << " ";
return 0;
}
다익스트라의 시간복잡도는 어떻게 될까? 코드를 살펴보자. N-1번 만큼 반복을 하고 있고, 각각의 경우 최소비용노드를 찾을때 N번 만큼 반복하고 있다. 여기서 N은 노드의 수(V)를 말한다. 즉, 이 방법의 시간복잡도는 O(V^2)다. 노드의 수가 많아질수록 비효율적이다. 대안으로 우선순위 큐로 구현하는 방법이 있다.
3. 다익스트라 우선순위 큐(priority queue) 버전
우선순위 큐로 구현할 때는 visit 배열이 필요 없다. 또한 다른 버전의 get_small_node()의 기능을 우선순위 큐가 대신하기 때문에 get_small_node() 함수도 필요 없다. 우선순위 큐 버전으로 다익스트라 구현시 필요 배열은 아래와 같다.
[ 다익스트라 구현시 필요 요소 ]
1. 노드 정보 벡터 nodes
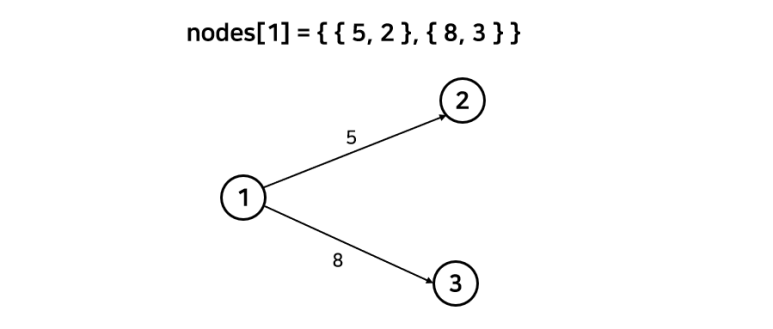
각 노드마다 연결되어 있는 모드 노드와 비용 정보를 나타내는 벡터다.
pair<int, int>를 원소로 가지며 원소 형태는 {비용, 목적지 노드} 이다.
nodes[1] = {{5,2}, {8,3}} // 노드1 -> 노드2 (비용 = 5) , 노드1 -> 노드3 (비용 = 8)
2. 시작점~노드 배열 dist
시작 노드로부터 각 노드까지의 비용 배열이다.
dist[1] = 3 // 시작점~노드1 까지 가는데 비용이 총 3만큼 든다.
dist[2] = 5 // 시작점~노드2 까지 가는데 비용이 총 5만큼 든다.
dist[5] = INF // 시작점~노드5 까지 가는데 비용이 무한이다.
3. 우선순위 큐 pq
간선 정보를 저장한다.
pair<int, int>를 원소로 가지며 원소 형태는 {비용, 목적지 노드} 이다.
원소.first 기준 내림차순으로 pop 되는 특징이 있다.
다른 버전의 get_small_node() 역할을 대신한다.노드 정보 벡터가 약간 헷갈릴 수 있는데 아래 그림을 참고하길 바란다.
이제 알고리즘을 살펴보자.
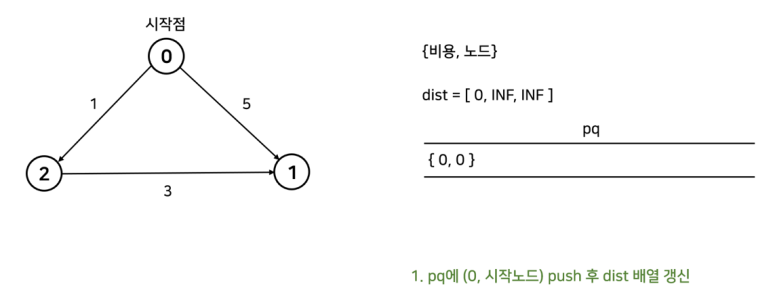
1. dist 배열을 전부 INF로 초기화하고 노드 정보를 모두 입력해준다
2. dist[시작노드] = 0 으로 값 갱신
3. pq에 {0, 목적지노드} push
4. pq.empty() 일때까지 다음을 반복
-- pq.front() = {비용, 노드}에 대해
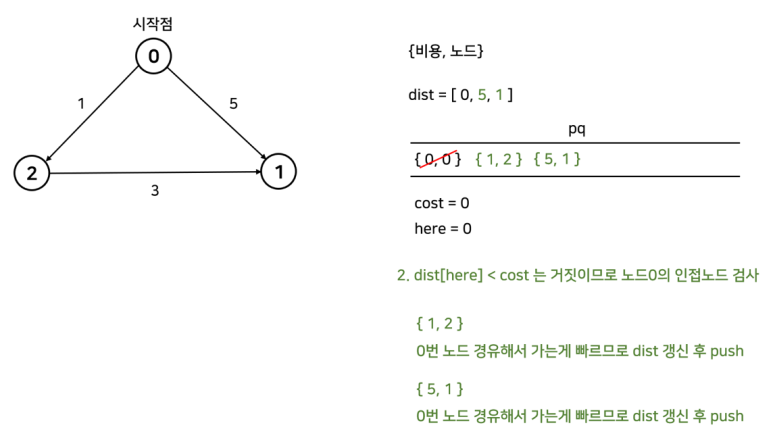
---- 1) dist[노드] < 비용 이면 skip
→ 이미 노드까지의 최소비용을 알고 있다는 뜻이기 때문
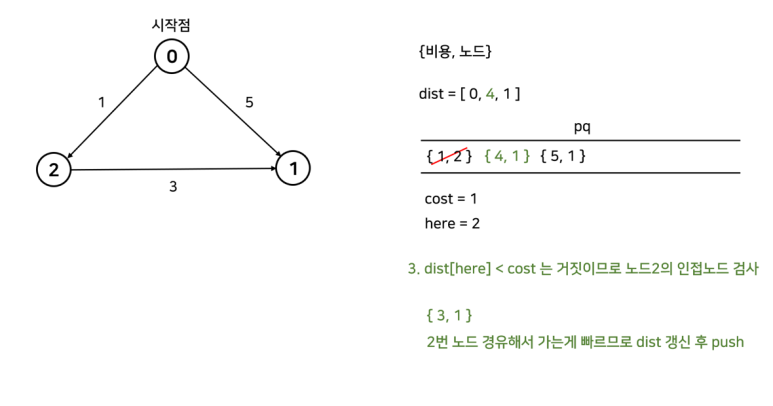
---- 2) 노드의 모든 인접 노드 검사
→ 자기를 거쳐가는게 빠르면 비용 갱신 후 {갱신한 비용, 인접노드} 큐에 push
간단한 예시로 알아보자.

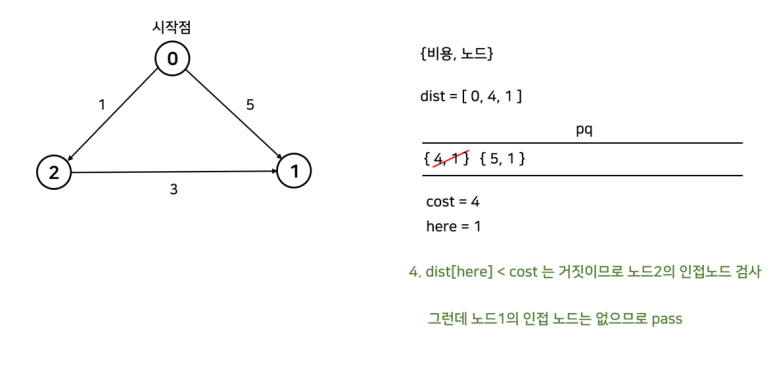
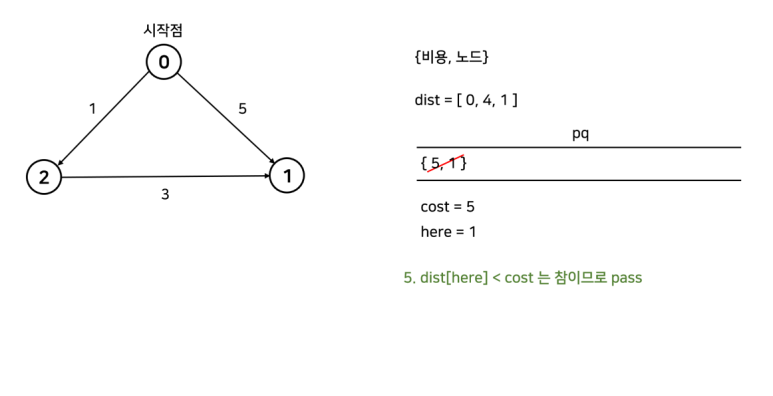
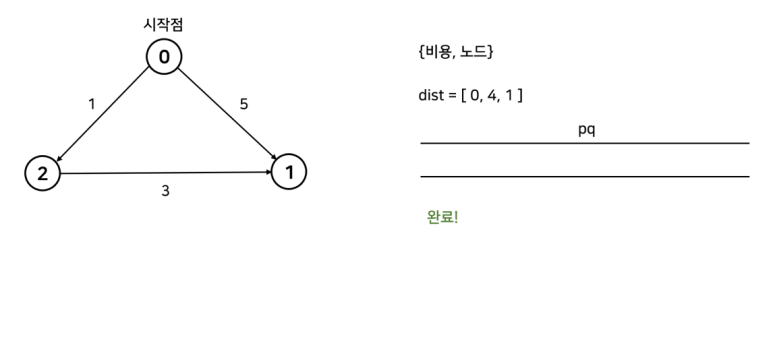
코드는 아래와 같다.
#include <iostream>
#include <vector>
#include <queue>
#define INF 1000000000
#define N 3
using namespace std;
vector<pair<int, int>> nodes[N];
int dist[N];
void dijkstra(int start) {
priority_queue<pair<int, int>> pq;
pq.push({ 0, start });
dist[start] = 0;
while (!pq.empty()) {
int cost = -pq.top().first; // 우선순위큐는 내림차순 정렬이기 때문
int here = pq.top().second;
pq.pop();
// 이미 최단거리 정보 있으면 pass
if (dist[here] < cost) continue;
for (int i = 0; i < nodes[here].size(); i++) {
int via_cost = cost + nodes[here][i].first;
// here을 경유해서 가는게 빠르면 dist 갱신 후 push
if (via_cost < dist[nodes[here][i].second]) {
dist[nodes[here][i].second] = via_cost;
pq.push({ -via_cost, nodes[here][i].second });
// 내림차순 정렬이라서 최소값이 가장 앞에 오도록 하기 위해 음수로 변환
}
}
}
}
int main() {
for (int i = 0; i < N; i++)
dist[i] = INF;
nodes[0].push_back({ 5, 1 });
nodes[0].push_back({ 1, 2 });
nodes[2].push_back({ 3, 1 });
dijkstra(0);
for (int i = 0; i < N; i++)
cout << dist[i] << endl;
return 0;
}
시간복잡도를 알아보자. 최단거리 노드는 우선순위 큐에서 자동으로 탐색해준다. 그런데 우선순위 큐는 힙 자료구조를 기반으로 하기 때문에 O(logN)의 시간복잡도를 가진다. 최악의 경우 큐의 크기는 엣지(E)의 개수와 같다. E개를 계속 탐색해서 삭제 및 추가를 진행하면 O(ElogE)의 시간 복잡도를 가진다고 할 수 있다.
4. 다익스트라의 한계
다익스트라 알고리즘은 노드의 재방문을 허용하지 않기 때문에 음수 간선이 존재할 경우 사용할 수 없다. 음수 간선이 존재하면 노드의 재방문을 고려해줘야 하므로 다익스트라 알고리즘에 위배된다. 아래 예시를 살펴보자.
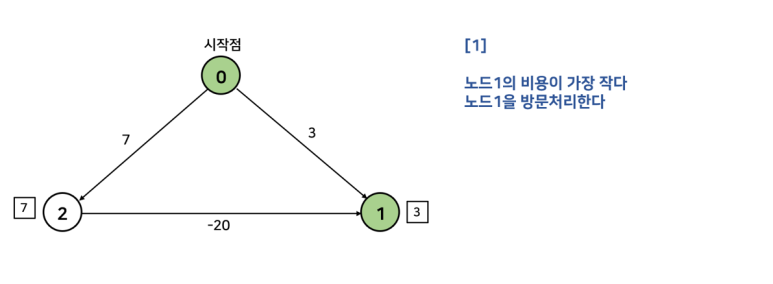
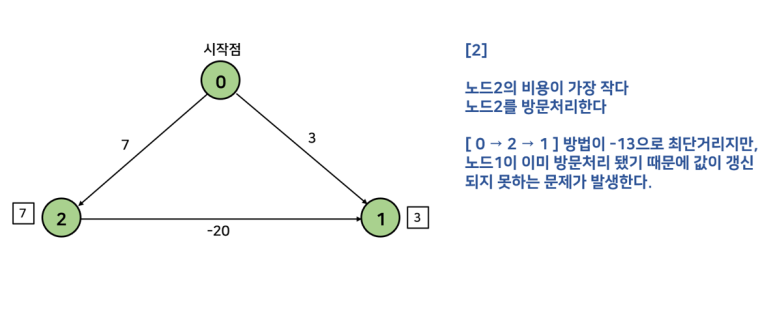
다익스트라 알고리즘은 최소 거리에 최소 거리를 붙여가며 값을 갱신하는 그리디 알고리즘의 일종의이기 때문에, 모든 가중치가 0 이상임이 보장되면 이미 방문한 노드의 비용은 그 값이 최소값임을 보장할 수 있다. 그러나 음수 가중치가 존재하면 위 그림처럼 이미 방문한 노드의 비용이 최소값임을 보장할 수 없다.
음수 간선이 존재할 경우 두 가지 대안이 있다.
1. 벨만-포드 알고리즘
2. SPFA 알고리즘
두 방법에 대해서는 따로 정리하도록 하겠다.
'CS > 알고리즘' 카테고리의 다른 글
| [C++] 투 포인터로 연속 부분합 구하기 (0) | 2022.01.14 |
|---|---|
| [C++] 위상 정렬(Topology Sort) (0) | 2022.01.14 |
| [C++] 중위 표기식을 후위 표기식으로 변환 후 계산 (0) | 2022.01.14 |
| [C++] 순열과 조합 DFS로 구현해보기 (1) | 2022.01.14 |
| [C++] Next Permutation, Prev Permutation 파헤치기 (0) | 2022.01.14 |



