1. 이분탐색 원리
이분탐색은 오름차순 또는 내림차순으로 정렬된 배열에 적용 가능한 탐색 기법이다. 정렬된 배열에서 특정 값을 찾을 때 정중앙에 위치한 값을 활용하면 아주 빠른 속도로 탐색을 끝낼 수 있다.
아래 그림을 보자. 배열은 오름차순으로 정렬되어 있다고 가정한다. 배열의 시작점과 끝점의 정중앙에 위치한 값을 '중앙값'이라고 부르겠다. 만약에 그림과 같이 '탐색값 < 중앙값' 이면 중앙값의 오른쪽 부분은 고려할 필요가 없다. 오름차순으로 정렬되어 있기 때문이다.

따라서 이제 끝점은 중앙값이서 1을 뺀 위치가 된다. 끝점의 위치가 이동했으므로 중앙값의 위치도 아래 그림과 같이 이동한다.

이번에는 '중앙값 < 탐색값' 이므로 중앙값의 왼쪽 부분은 볼 필요가 없다. 따라서 시작점은 중앙값에 1을 더해준 위치가 된다. 이러한 과정을 반복하면 탐색값을 빠르게 찾을 수 있다. 시작점이 끝점보다 커질때까지 탐색을 진행하면 된다. 나머지는 스스로 해보길 바란다.
이렇게 이분탐색은 중앙값을 기준으로 절반씩 버려진다. 매 단계마다 절반씩 버려지므로 이분 탐색의 시간 복잡도는 log_2(n)이다.
2. 손으로 직접 해보기
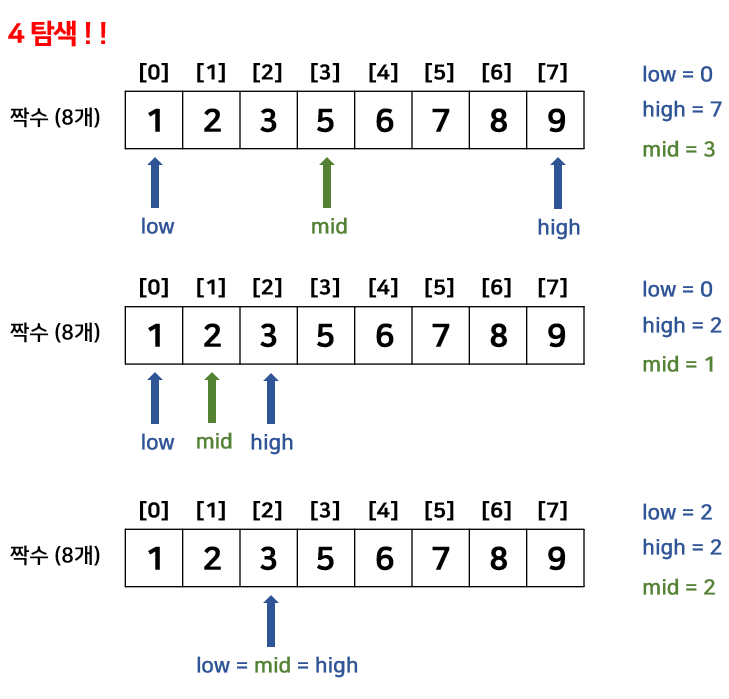
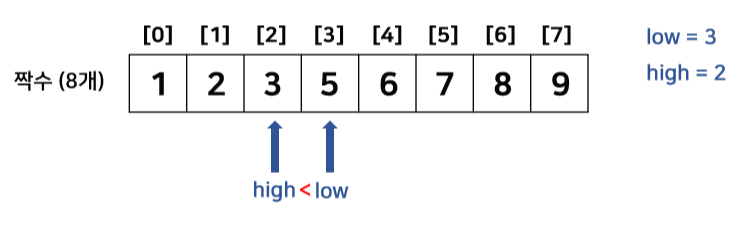
배열의 크기가 홀수일 때와 짝수일 때, 탐색값이 존재하지 않는 경우로 나눠서 살펴보자. 배열의 크기가 홀수일 때와 짝수일 때를 굳이 나누는 이유는 중앙값의 위치가 홀수일때는 정중앙이지만 짝수일때는 그렇지 않아서 이를 궁금해 하는 사람이 있을까봐 그런거다. 결론을 먼저 말하면 차이 없다. 하지만 눈으로 직접 확인하는게 정확하다. 시작점은 low, 끝점은 high, 중앙값의 위치는 mid로 표현했다.
1) 배열의 크기가 홀수 (탐색값 = 3)

2) 배열의 크기가 짝수 (탐색값 = 3)

3) 탐색값이 존재하지 않는 경우 (탐색값 = 4)
3. 구현
이분탐색의 구현은 크게 어렵지 않다. 위 과정을 그대로 구현하면 된다. 나는 배열을 사용하지 않고 벡터를 사용했다. 설명은 주석 참고!
int binary_search(vector<int>& v, int num) {
int low = 0; // 시작점
int high = v.size() - 1; // 끝점
int idx = -1; // 반환 인덱스
while (low <= high) {
int mid = (low + high) / 2; // 중앙값 위치
// 1. 탐색값을 찾으면 멈춘다
// 2. 탐색값 < 중앙값 -> 끝점 갱신
// 3. 중앙값 > 탐색값 -> 시작점 갱신
if (v[mid] == num) {
idx = mid;
break;
}
else if (num < v[mid]) high = mid - 1;
else if (v[mid] < num) low = mid + 1;
}
return idx;
}
4. lower_bound & upper_bound
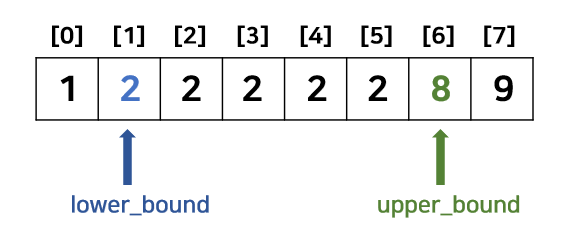
lower_bound는 정렬된 배열에서 탐색값이 2개 이상 있는 경우 가장 앞에 위치한 탐색값을 의미하고, upper_bound는 가장 뒤에 위치한 탐색값의 다음 위치를 의미한다.
STL vector에 이 함수가 정의되어 있어 사용 방법을 알아보자. 이 둘은 이분탐색을 기반으로 하기 때문에 오름차순으로 정렬되어 있어야 사용할 수 있다.
auto lower = lower_bound(vec.begin(), vec.end(), key);
-> 벡터에서 최초의 key 이상의 값을 iterator 형태로 저장
auto upper = upper_bound(vec.begin(), vec.end(), key);
-> 벡터에서 최초의 key 초과값을 iterator 형태로 저장
반환값은 iterator이기 때문에 인덱스를 알고 싶으면 vec.begin() 을 빼주면 된다. 만약에 *iterator를 출력하면 key 값을 출력할 것이다. 위 그림을 예로 들면 key = 2 로 설정했을때 *lower_bound의 값은 2, *upper_bound의 값은 8이 된다. 만약에 두 값의 인덱스를 확인하고 싶으면 아래와 같이 하면 된다.
vector<int> vec = {1,2,2,2,2,2,8,9};
cout << lower_bound(vec.begin(), vec.end(), 2) - vec.begin() << endl; // 1 출력
cout << upper_bound(vec.begin(), vec.end(), 2) - vec.begin() << endl; // 6 출력
'CS > 알고리즘' 카테고리의 다른 글
| [C++] 투 포인터로 연속 부분합 구하기 (0) | 2022.01.14 |
|---|---|
| [C++] 위상 정렬(Topology Sort) (0) | 2022.01.14 |
| [C++] 다익스트라(Dijkstra) (0) | 2022.01.14 |
| [C++] 중위 표기식을 후위 표기식으로 변환 후 계산 (0) | 2022.01.14 |
| [C++] 순열과 조합 DFS로 구현해보기 (1) | 2022.01.14 |



