1. Next Permutation
알고리즘 문제를 풀다 보면 <algorithm> 라이브러리의 next_permutation 함수를 쓸 일이 많다. 문득 이 함수의 원리가 궁금해서 이 글에 정리해보려고 한다. Next permutation의 기본 원리는 오름차순을 내림차순으로 변경하는 것이다. 변경하는 과정에서 모든 가능한 조합이 나오게 된다. 단, 수열은 사전에 오름차순 정렬되어 있어야 한다. Next_permutation의 과정을 살펴보면 아래와 같다.
Next Permutation 과정
1. find max(k), a[k] < a[k+1]
2. find max(m), a[k] < a[m] && k < m
3. swap(a[k], a[m])
4. reverse(a[k+1:])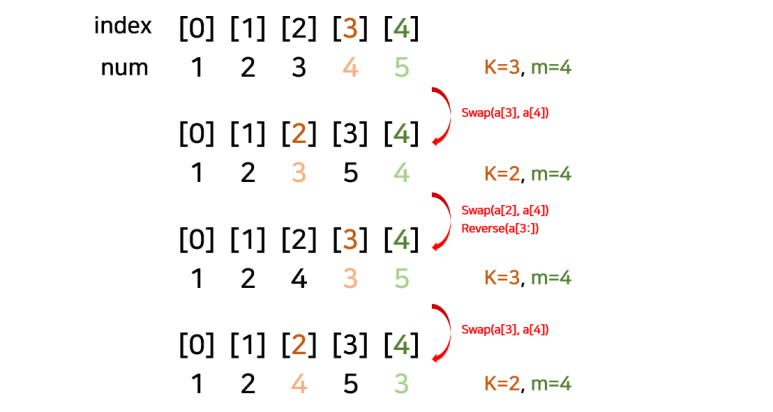
[1, 2, 3, 4, 5]를 수동으로 한 예시다. 이런식으로 계속 반복하면 최종적으로 [5, 4, 3, 2, 1] 형태가 된다. 1번 과정을 쭉 돌렸을 때 찾을 수 없으면 모든 가능한 조합을 한번 돌린 것이므로, 이를 다시 reverse 시켜 원본 형태를 반환한다. 우선 수동으로 한 예시를 코드 결과와 비교해보자.
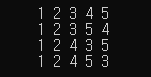
수동으로 한 것과 일치한다!! 이제 코드로 구현해보자. next_permutation의 과정 네 단계를 그대로 구현하면 된다. 1번 과정을 성공하면 4번까지 진행한 뒤에 true를 반환해주고, 1번 과정을 실패하면 수열을 뒤집은 다음에 false를 반환하면 된다. 아래는 구현한 코드다. 입력 파리미터는 배열 a와 크기 size다. 시간 복잡도는 O(n)이다.
#include <iostream>
#include <algorithm>
using namespace std;
bool next_permutation(int a[], int size) {
// 1. find max(k), a[k] < a[k+1]
int k = size - 1; // 가장 끝 인덱스
int m = size - 1;
while (k > 0 && a[k - 1] >= a[k]) k--;
if (k == 0) {
// 더이상 오름차순이 없으면 뒤집고 종료
reverse(a, a + size);
return false;
}
else {
// 2. find max(m), a[k] < a[m] && k < m
while (a[k - 1] >= a[m]) m--;
// 3. swap(a[k], a[m])
swap(a[k - 1], a[m]);
// 4. reverse(a[k + 1:])
reverse(a + k, a + size);
return true;
}
}
int main() {
int a[5] = { 1,2,3,4,5 };
do {
for (int i = 0; i < 5; i++)
cout << a[i] << " ";
cout << endl;
} while (next_permutation(a, 5));
return 0;
}2. Prev Permutation
Prev permutation은 next permutation과 정반대다. Next permutation은 오름차순 → 내림차순으로 변경해주는 과정이라고 할 수 있다. prev permutation 내림차순 → 오름차순으로 변경해주면 끝이다. Next Permutation에서 1,2 단계 부등호를 반대로 바꿔주기만 하면 된다.
#include <iostream>
#include <algorithm>
using namespace std;
bool next_permutation(int a[], int size) {
// 1. find max(k), a[k] < a[k+1]
int k = size - 1; // 가장 끝 인덱스
int m = size - 1;
while (k > 0 && a[k - 1] <= a[k]) k--;
if (k == 0) {
// 더이상 오름차순이 없으면 뒤집고 종료
reverse(a, a + size);
return false;
}
else {
// 2. find max(m), a[k] < a[m] && k < m
while (a[k - 1] <= a[m]) m--;
// 3. swap(a[k], a[m])
swap(a[k - 1], a[m]);
// 4. reverse(a[k + 1:])
reverse(a + k, a + size);
return true;
}
}
int main() {
int a[5] = { 5,4,3,2,1 };
do {
for (int i = 0; i < 5; i++)
cout << a[i] << " ";
cout << endl;
} while (next_permutation(a, 5));
return 0;
}
이제 next_permutation과 prev_permutation 사용법은 헷갈리지 않을 것 같다 : )
'CS > 알고리즘' 카테고리의 다른 글
| [C++] 다익스트라(Dijkstra) (0) | 2022.01.14 |
|---|---|
| [C++] 중위 표기식을 후위 표기식으로 변환 후 계산 (0) | 2022.01.14 |
| [C++] 순열과 조합 DFS로 구현해보기 (1) | 2022.01.14 |
| [C++] 최소비용신장트리 - kruskal 알고리즘 (0) | 2022.01.14 |
| [C++] 합집합 찾기(Union-Find) (0) | 2022.01.14 |



