https://www.acmicpc.net/problem/1038
1038번: 감소하는 수
음이 아닌 정수 X의 자릿수가 가장 큰 자릿수부터 작은 자릿수까지 감소한다면, 그 수를 감소하는 수라고 한다. 예를 들어, 321과 950은 감소하는 수지만, 322와 958은 아니다. N번째 감소하는 수를
www.acmicpc.net
문제를 읽고 그냥 감소하는 수를 다 구하고 오름차순 정렬하면 될 것 같았다. 재귀 함수로 구현할 수 있는 문제다. 아래의 아이디어를 아주 약간만 응용하면 된다.
현재 숫자는 X
X의 1의 자리 숫자는 k
X * 10 + (k - α) 는 항상 감소하는 수다.
이제 감소하는 수를 구하는 함수 get_dec()를 살펴보자.
void get_dec(long now, int last){
for(int i = last - 1; i >= 0; i--){
dec_nums.push_back(now * 10 + i);
get_dec(now * 10 + i, i);
}
}
위 아이디어를 그대로 구현한 것이다. 일의 자리 숫자보다 작은 모든 숫자를 뒤에 붙여주는 함수다.
문제를 풀 때는 아무 생각 없었는데, 감소하는 수는 과연 몇 개일까? 수학적으로 한번 구해보자.
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
사용 가능한 숫자는 0~9까지 총 열 개다. 여기서 뽑고 싶은 숫자를 아무거나 뽑아보자. 나는 1, 6, 7, 9를 뽑았다. 이 숫자로 만들 수 있는 감소하는 수는 9761로 딱 한 가지 경우밖에 없다. 아마 어떻게 뽑아도 마찬가지일 것이다. 그 이유는 감소하는 수에는 중복되는 숫자가 없고, 모든 숫자가 내림차순으로 정렬되어 있기 때문이다.
따라서 문제는 10개의 숫자 중에서 n개를 뽑는 경우의 수, '조합' 문제로 바뀐다. 가능한 모든 경우의 수는 아래와 같다.
10_C_1
10_C_2
10_C_3
10_C_4
10_C_5
10_C_6
10_C_7
10_C_8
10_C_9
10_C_10
여기서 잠시 고등학생때 배운 개념이 등장한다. 이항정리....기억하시나요.... 나는 까먹어서 찾아봤다.
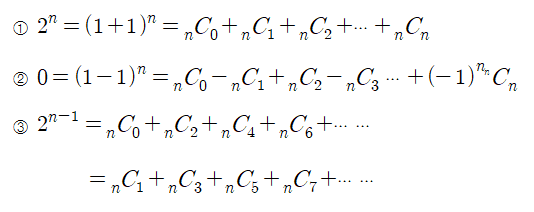
1번 공식에 의해 10_C_1 ~ 10_C10 까지의 합은 2^10 - 1 임을 알 수 있다. 왜냐하면 n_C_0이 좌변으로 가기 때문이다. 따라서 감소하는 수는 총 1023개임을 알 수 있다.
여기까지는 그냥 궁금해서 끄적여봤다. 정답 코드는 아래와 같다. 참고로 마지막 감소하는 숫자가 30억을 넘어가서 자료형을 조심해야 한다. int로 하면 틀리고 최소 long으로 해야 한다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// 자료형에 주의해야 한다. int -> long
int N;
vector<long> dec_nums;
void get_dec(long now, int last){
for(int i = last - 1; i >= 0; i--){
dec_nums.push_back(now * 10 + i);
get_dec(now * 10 + i, i);
}
}
int main(){
cin >> N;
for(int i = 0; i <= 9; i++){
dec_nums.push_back(i);
get_dec(i, i);
}
sort(dec_nums.begin(), dec_nums.end());
if(N >= dec_nums.size())
cout << -1 << endl;
else
cout << dec_nums[N] << endl;
return 0;
}'알고리즘 문제풀이 > 추천 문제' 카테고리의 다른 글
| [ 백준 1260 ] DFS와 BFS (C++) (0) | 2022.01.24 |
|---|---|
| [ 백준 17070 ] 파이프 옮기기 1 (C++) (0) | 2022.01.23 |
| [ 백준 2667 ] 단지번호붙이기 (C++) (0) | 2022.01.20 |
| [ 백준 2294 ] 동전2 (C++) (0) | 2022.01.20 |
| [ 백준 2293 ] 동전1(C++) (0) | 2022.01.17 |

