이진 트리는 모든 노드가 최대 두 개의 자식 노드를 갖는 트리다. 아래와 같은 특징을 갖는다.
1. 각 노드는 최대 2개의 자식을 갖는다.
2. 각 노드의 자식은 왼쪽 자식과 오른쪽 자식으로 구분된다.
이진 트리는 왼쪽 자식과 오른쪽 자식을 엄격하게 구분한다. 이게 무슨 뜻이냐 하면 원소가 같아도 위치에 따라 다른 트리로 분류될 수 있다는 뜻이다. 예를 들어 아래 두 개의 트리는 서로 다른 이진 트리다.

이진 트리는 그 구조에 따라 다섯 가지 유형으로 나뉜다. 하나씩 살펴보자.
이진 트리 종류
1. 포화 이진 트리(Perfect Binary Tree)
: 모든 중간 노드가 두 개의 자식을 가지는 이진 트리. 포와 이진 트리에서 Level n 의 노드 수는 (2^n) 이라는 특징이 있다.

2. 완전 이진 트리(Complete Binary Tree)
: 마지막 레벨을 제외하고 모든 레벨이 완전히 채워진 이진 트리. 마지막 레벨은 왼쪽부터 차례대로 채워져야 한다.

3. 전 이진 트리(Full Binary Tree)
: 모든 노드가 0개 또는 2개의 자식을 가지는 이진 트리. 자식이 한 개인 노드가 하나라도 있으면 전 이진 트리가 아니다.

4. 편향 이진 트리(Skewed Binary Tree)
: (노드의 개수 = 트리의 높이) 를 만족하는 트리.

5. 균형 이진 트리(Balanced Binary Tree)
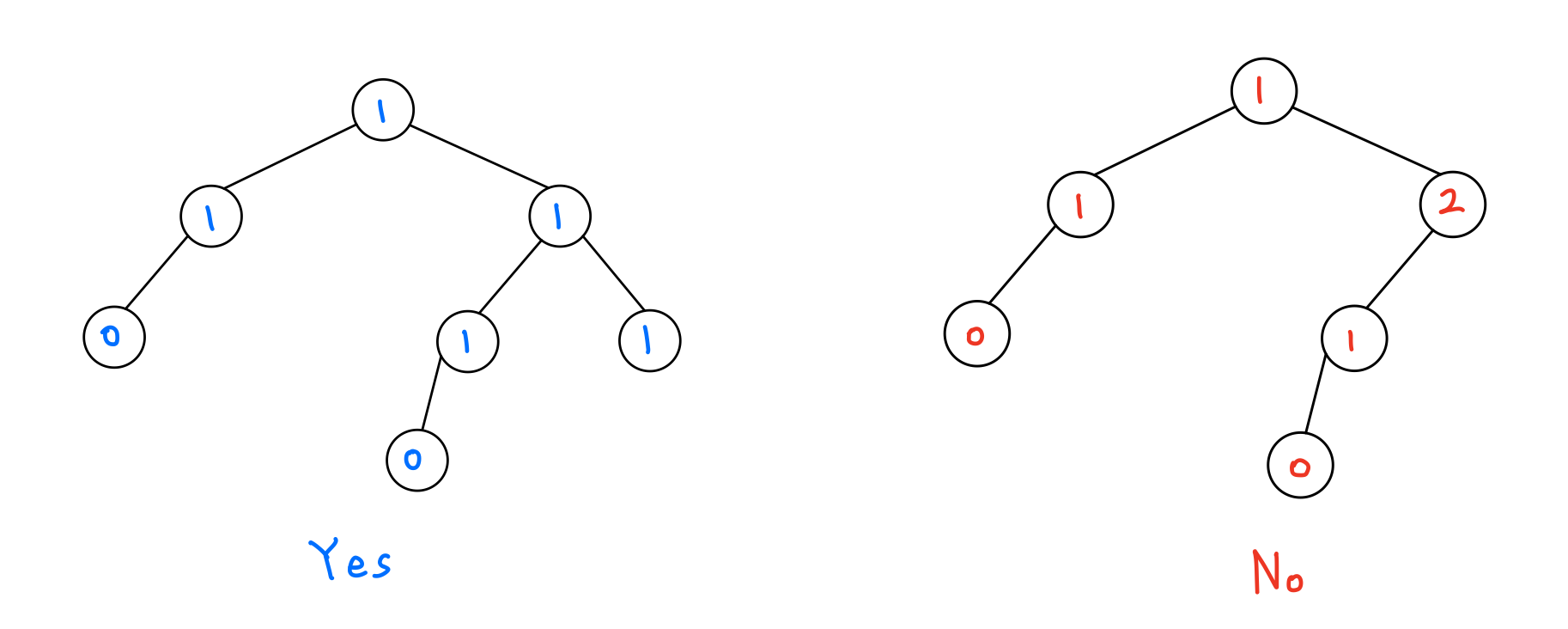
: 모든 좌, 우 서브트리의 높이차가 1 이하인 트리. 그림에서 모든 노드의 값은 좌우 서브트리의 높이차를 의미한다. 오른쪽 트리를 보면 좌우 서브 트리의 높이차가 2인 노드가 있으므로 균형 이진 트리가 아니다.
이진 트리 순회의 세 가지 방법
이진 트리의 모든 노드를 검사하는 것을 '순회'라고 한다. 이진 트리에서 모든 노드를 거치는 대표적인 순회 방법 세 가지를 소개한다. 먼저 개념을 살펴보고, 예제를 풀어보자.
이진 트리의 모든 노드는 최대 두 개의 노드만 가지므로 이동 규칙은 '왼쪽 자식 → 오른쪽 자식' 이 전부다. 순회는 '이동' 또는 '현재 노드 방문' 두 가지 액션만 취하기 때문에 '현재 노드 방문'을 어디 넣냐에 따라 전위, 중위, 후위 순회로 나뉜다. 따라서 순회는 세 가지 규칙에 따라 순차적으로 진행되는데, 재귀적으로 실행되기 때문에 새로운 노드로 갈때마다 첫 번째 규칙부터 다시 시작한다. 이를 인지한 상태에서 아래의 순회 규칙을 보고 출력 순서를 직접 도출해보자.
순회의 시작점은 항상 루트 노드가 된다. 우리가 탐색을 진행할 트리 구조는 아래와 같다. 순회 방식에 따라 출력 순서가 어떻게 변하는지 살펴보자.

1. 전위 순회
1) 현재 노드 방문
2) 왼쪽 자식으로 이동
3) 오른쪽 자식으로 이동

출력 순서 : 1-2-4-8-9-5-10-11-3-6-12-13-7-14-15
2. 중위 순회
1) 왼쪽 자식으로 이동
2) 현재 노드 방문
3) 오른쪽 자식으로 이동

출력 순서 : 8-4-9-2-10-5-11-1-12-6-13-3-14-7-15
3. 후위 순회
1) 왼쪽 자식으로 이동
2) 오른쪽 자식으로 이동
3) 현재 노드 방문

출력 순서 : 8-9-4-10-11-5-2-12-13-6-14-15-7-3-1
예제를 통한 순회 구현
백준 1991번은 순회를 구현하는 문제다. 문제를 한 번 읽고 오기를 바란다. 문제를 수월하게 풀기 위해서는 아래와 같이 좌, 우 자식값을 저장할 수 있는 구조체를 정의해야 한다.
struct Node{
char left;
char right;
};
문제에서 '노드의 이름은 A부터 차례대로 알파벳 대문자로 매겨지며, 항상 A가 루트 노드가 된다'라고 했으므로 모든 노드는 배열의 인덱스로 접근 가능하다. 모든 대문자에 65를 빼면 A는 0, B는 1. C는 2, D는 3 ... 이렇게 대응되기 때문이다. 따라서 Node를 원소로 가지는 크기가 26인 배열을 생성하고, 입력값을 아래와 같이 처리하면 배열은 사실상 트리 구조를 가지게 된다.
Node ary[26]; // Node 배열
cin >> me >> l >> r; // char 입력
ary[me - 65].left = l;
ary[me - 65].right = r;
전위 순회, 중위 순회, 후위 순회는 아까 위에서 설명한 순서 그대로 적으면 된다. 다만 재귀적으로 실행되기 때문에 기저 조건만 정확하게 적어주면 된다. 문제에서 자식 노드가 없는 경우 '.' 으로 표현한다고 했으므로 기저 조건은 현재 노드가 '.' 일때다. 이를 기반으로 세 가지 순회 함수를 작성해 보자.
// 전위 순회
void preOrder(char node){
if(node == '.') return;
cout << node;
preOrder(ary[node - 65].left);
preOrder(ary[node - 65].right);
}
// 중위 순회
void inOrder(char node){
if(node == '.') return;
inOrder(ary[node - 65].left);
cout << node;
inOrder(ary[node - 65].right);
}
// 후위 순회
void postOrder(char node){
if(node == '.') return;
postOrder(ary[node - 65].left);
postOrder(ary[node - 65].right);
cout << node;
}
크게 어려운 개념은 아니기 때문에 이해하는데 무리는 없을 것이다.
오늘은 여기서 마무리!! 다음 글은 '이진 탐색 트리'로 다시 돌아오겠다.
'CS > 자료구조' 카테고리의 다른 글
| [ 자료구조 ] 이진 탐색 트리(Binary Search Tree) (0) | 2022.03.28 |
|---|---|
| [ 자료구조 ] 트리 용어 정리 (0) | 2022.03.23 |
| [ 자료구조 ] 큐(Queue) (0) | 2022.03.17 |
| [ 자료구조 ] 스택(Stack) (0) | 2022.03.09 |
| [ 자료구조 ] 연결 리스트 : 원형 연결 리스트 (0) | 2022.03.07 |



